NOBのArduino日記！

NOBのArduino日記！

趣味は車・バイク・自転車・ラジコン・電子工作です。

MARGセンサーから三次元姿勢推定！(Madgwickフィルターとは)

便利 #工学
イメージ 3
マルチ機能(MARG)センサー(ATD-M4S,GY-80)

 先日使った上図のMARGセンサー(xyz角速度・xyz加速度・xyz地磁気の計9軸)から得られたデータを元に、ドローンの現在の姿勢を推定したいです。
 セバスチャンO.H.マッジウィックさんが考案された「Madgwickフィルター※1」と言う凄いフィルターが公開されていましたので、まとめてみました！ムズカシイ！

※1：引用文献「An efficient orientation filter for inertial and inertial/magnetic sensor arrays_Sebastian O.H. Madgwick(April 30, 2010)」

1. Madgwickフィルターとは

 Madgwickフィルターとは、相補フィルターの一種。
 3軸角速度計と3軸加速度計からなるIMU(慣性計測装置、英: inertial measurement unit)と、さらに3軸地磁気計も追加したMARG(英：Magnetic, Angular Rate and Gravity)に適用可能な方位フィルタの事。
 各センサーには以下に示す長所と短所が有り、それぞれの短所をそれぞれの長所で相互に補う事で三次元姿勢推定精度を向上させています。

〇加速度計の長所「準静的な運動において重力方向から傾斜角を推定できる」
〇加速度計の短所「センサ動特性による遅れが発生する」
〇角速度計の長所「動的な姿勢変化を測定できる」
〇角速度計の短所「姿勢を求める際の積分に伴い誤差が累積する」
〇地磁気計の長所「初期の地磁気方向と現在の出力の照合により方位を推定できる」
〇地磁気計の短所「周辺環境の磁気外乱が影響する」

 具体的にMARGの場合には、磁気歪みおよび角速度計バイアスドリフト補償が組み込まれています。
 このフィルタはクォータニオン(四元数)表現を使用して、加速度計データと地磁気計データを解析的に導出し、最適化された勾配降下アルゴリズムを使用して角速度計測定誤差の方向を四元数導関数として図1の様に計算します。

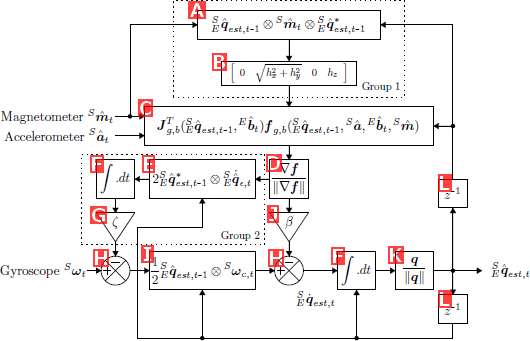
イメージ 5
図1：磁気ひずみ(Group1)及び角速度計ドリフト(Group2)補償を含む
MARGのための方向フィルタブロック図

〇図1 A～L関数が持つ機能(※1文献を読んだ私の理解)です間違ってたらご指摘ください
　A ：地磁気の傾きによる誤差を補正
　B ：地球を基準とした方向にx・z軸成分のみ正規化
　C ：勾配降下法によるアルゴリズムによって最適化
　D ：方位の推定変化率
　E ：姿勢変化率の推定誤差の正規化された方向(ｼﾞｬｲﾛｽｺｰﾌﾟの各軸の角度誤差)
　F ：時間で積分
　G ：加速度計の誤差積分値に対する利得(重み付け) 
　H ：四元数積(方位の積を計算)
　I ：時刻tにおける地球を基準としたセンサの向き(推定値)
　J ：平均をゼロとした全ての加速度計測定誤差によるフィルタの利得。 
　K ：推定した方位
　L ：推定した方位を次計算へフィードバック

2. Madgwickフィルターの利点

 IMU(6軸)やMARG(9軸)から姿勢を推定するフィルターとして、代表的な物に「Kalmanフィルター」が有ります。
 これと比較して、今回検討している「Madgwickフィルター」が持つ利点を以下2.1～2.4に示します。

2.1 計算負荷が軽い
 反復の無い勾配降下法を使用する事で、IMUで109回、MARGで277回(図2参照)と、少ない演算回数でフィルタの更新が可能。
/*引用元「An efficient orientation filter for inertial and inertial/magnetic sensor arrays」Sebastian O.H. Madgwick(April 30, 2010)」*/

#include <math.h>  //'sqrt'に数学ライブラリが必要 
/*システム定数*/
#define deltat 0.001f // 1秒間のサンプリング周期（秒単位）
#define gyroMeasError 3.14159265358979 * (5.0f / 180.0f) //角速度計の測定誤差（rad / s）（5 deg / sと表示）
#define gyroMeasDrift 3.14159265358979 * (0.2f / 180.0f) //角速度計測定誤差（rad / s / s）（0.2f deg / s / sとして示す）
#define beta sqrt(3.0f / 4.0f) * gyroMeasError // ベータを計算する
#define zeta sqrt(3.0f / 4.0f) * gyroMeasDrift // ゼータを計算する
/*グローバルシステム変数*/
float a_x, a_y, a_z; // 加速度計の測定
float w_x, w_y, w_z; // 角速度計のrad / s単位の測定
float m_x, m_y, m_z; // 地磁気計の測定
float SEq_1 = 1, SEq_2 = 0, SEq_3 = 0, SEq_4 = 0; // 初期条件付き推定方位四元数要素
float b_x = 1, b_z = 0; // 地球フレームにおけるフラックスの基準方向
float w_bx = 0, w_by = 0, w_bz = 0; // 推定角速度計バイアス誤差

/*1つのフィルタ反復を計算する関数*/
void filterUpdate(float w_x, float w_y, float w_z, float a_x, float a_y, float a_z, float m_x, float m_y, float m_z){
  /*ローカルシステム変数*/
 float norm; // ベクトルノルム
 float SEqDot_omega_1, SEqDot_omega_2, SEqDot_omega_3, SEqDot_omega_4; // 角速度計要素からの四元数
 float f_1, f_2, f_3, f_4, f_5, f_6; // 目的関数要素
 float J_11or24, J_12or23, J_13or22, J_14or21, J_32, J_33, J_41, J_42, J_43, J_44, J_51, J_52, J_53, J_54, J_61, J_62, J_63, J_64; //目的関数ヤコビ行列要素
 float SEqHatDot_1, SEqHatDot_2, SEqHatDot_3, SEqHatDot_4; //角速度計誤差の推定方向
 float w_err_x, w_err_y, w_err_z; // 角速度計誤差の推定方向（角度）
 float h_x, h_y, h_z; // 地球フレームにおける計算されたフラックス
 /*再計算された計算を避けるためのaxulirary変数*/
 float halfSEq_1 = 0.5f * SEq_1;
 float halfSEq_2 = 0.5f * SEq_2;
 float halfSEq_3 = 0.5f * SEq_3;
 float halfSEq_4 = 0.5f * SEq_4;
 float twoSEq_1 = 2.0f * SEq_1;
 float twoSEq_2 = 2.0f * SEq_2;
 float twoSEq_3 = 2.0f * SEq_3;
 float twoSEq_4 = 2.0f * SEq_4;
 float twob_x = 2.0f * b_x;
 float twob_z = 2.0f * b_z;
 float twob_xSEq_1 = 2.0f * b_x * SEq_1;
 float twob_xSEq_2 = 2.0f * b_x * SEq_2;
 float twob_xSEq_3 = 2.0f * b_x * SEq_3;
 float twob_xSEq_4 = 2.0f * b_x * SEq_4;
 float twob_zSEq_1 = 2.0f * b_z * SEq_1;
 float twob_zSEq_2 = 2.0f * b_z * SEq_2;
 float twob_zSEq_3 = 2.0f * b_z * SEq_3;
 float twob_zSEq_4 = 2.0f * b_z * SEq_4;
 float SEq_1SEq_2;
 float SEq_1SEq_3 = SEq_1 * SEq_3;
 float SEq_1SEq_4;
 float SEq_2SEq_3;
 float SEq_2SEq_4 = SEq_2 * SEq_4;
 float SEq_3SEq_4;
 float twom_x = 2.0f * m_x;
 float twom_y = 2.0f * m_y;
 float twom_z = 2.0f * m_z;
 /*加速度計の測定値を正規化する*/
 norm = sqrt(a_x * a_x + a_y * a_y + a_z * a_z);
 a_x /= norm;
 a_y /= norm;
 a_z /= norm;
 /*地磁気計の測定値を正規化する*/
 norm = sqrt(m_x * m_x + m_y * m_y + m_z * m_z);
 m_x /= norm;
 m_y /= norm;
 m_z /= norm;
 /*目的関数とヤコビ行列を計算する*/
 f_1 = twoSEq_2 * SEq_4 - twoSEq_1 * SEq_3 - a_x;
 f_2 = twoSEq_1 * SEq_2 + twoSEq_3 * SEq_4 - a_y;
 f_3 = 1.0f - twoSEq_2 * SEq_2 - twoSEq_3 * SEq_3 - a_z;
 f_4 = twob_x * (0.5f - SEq_3 * SEq_3 - SEq_4 * SEq_4) + twob_z * (SEq_2SEq_4 - SEq_1SEq_3) - m_x;
 f_5 = twob_x * (SEq_2 * SEq_3 - SEq_1 * SEq_4) + twob_z * (SEq_1 * SEq_2 + SEq_3 * SEq_4) - m_y;
 f_6 = twob_x * (SEq_1SEq_3 + SEq_2SEq_4) + twob_z * (0.5f - SEq_2 * SEq_2 - SEq_3 * SEq_3) - m_z;
 J_11or24 = twoSEq_3;  //行列乗算が無効にされたJ_11
 J_12or23 = 2.0f * SEq_4;
 J_13or22 = twoSEq_1;  //行列乗算が無効にされたJ_12
 J_14or21 = twoSEq_2;
 J_32 = 2.0f * J_14or21; //行列乗算が否定された
 J_33 = 2.0f * J_11or24; // 行列乗算が否定された
 J_41 = twob_zSEq_3; // 行列乗算が否定された
 J_42 = twob_zSEq_4;
 J_43 = 2.0f * twob_xSEq_3 + twob_zSEq_1; // 行列乗算が否定された
 J_44 = 2.0f * twob_xSEq_4 - twob_zSEq_2; // 行列乗算が否定された
 J_51 = twob_xSEq_4 - twob_zSEq_2; // 行列乗算が否定された
 J_52 = twob_xSEq_3 + twob_zSEq_1;
 J_53 = twob_xSEq_2 + twob_zSEq_4;
 J_54 = twob_xSEq_1 - twob_zSEq_3; // 行列乗算が否定された
 J_61 = twob_xSEq_3;
 J_62 = twob_xSEq_4 - 2.0f * twob_zSEq_2;
 J_63 = twob_xSEq_1 - 2.0f * twob_zSEq_3;
 J_64 = twob_xSEq_2;
 /*勾配を計算する（行列乗算）*/
 SEqHatDot_1 = J_14or21 * f_2 - J_11or24 * f_1 - J_41 * f_4 - J_51 * f_5 + J_61 * f_6;
 SEqHatDot_2 = J_12or23 * f_1 + J_13or22 * f_2 - J_32 * f_3 + J_42 * f_4 + J_52 * f_5 + J_62 * f_6;
 SEqHatDot_3 = J_12or23 * f_2 - J_33 * f_3 - J_13or22 * f_1 - J_43 * f_4 + J_53 * f_5 + J_63 * f_6;
 SEqHatDot_4 = J_14or21 * f_1 + J_11or24 * f_2 - J_44 * f_4 - J_54 * f_5 + J_64 * f_6;
 /*勾配を正規化して角速度計誤差の方向を推定する*/
 norm = sqrt(SEqHatDot_1 * SEqHatDot_1 + SEqHatDot_2 * SEqHatDot_2 + SEqHatDot_3 * SEqHatDot_3 + SEqHatDot_4 * SEqHatDot_4);
 SEqHatDot_1 = SEqHatDot_1 / norm;
 SEqHatDot_2 = SEqHatDot_2 / norm;
 SEqHatDot_3 = SEqHatDot_3 / norm;
 SEqHatDot_4 = SEqHatDot_4 / norm;
 /*角速度計誤差の角度推定方向を計算する*/
 w_err_x = twoSEq_1 * SEqHatDot_2 - twoSEq_2 * SEqHatDot_1 - twoSEq_3 * SEqHatDot_4 + twoSEq_4 * SEqHatDot_3;
 w_err_y = twoSEq_1 * SEqHatDot_3 + twoSEq_2 * SEqHatDot_4 - twoSEq_3 * SEqHatDot_1 - twoSEq_4 * SEqHatDot_2;
 w_err_z = twoSEq_1 * SEqHatDot_4 - twoSEq_2 * SEqHatDot_3 + twoSEq_3 * SEqHatDot_2 - twoSEq_4 * SEqHatDot_1;
 /*角速度計のベイズを計算して除去する*/
 w_bx += w_err_x * deltat * zeta;
 w_by += w_err_y * deltat * zeta;
 w_bz += w_err_z * deltat * zeta;
 w_x -= w_bx;
 w_y -= w_by;
 w_z -= w_bz;
 /*角速度計によって測定された四元数を計算する*/
 SEqDot_omega_1 = -halfSEq_2 * w_x - halfSEq_3 * w_y - halfSEq_4 * w_z;
 SEqDot_omega_2 = halfSEq_1 * w_x + halfSEq_3 * w_z - halfSEq_4 * w_y;
 SEqDot_omega_3 = halfSEq_1 * w_y - halfSEq_2 * w_z + halfSEq_4 * w_x;
 SEqDot_omega_4 = halfSEq_1 * w_z + halfSEq_2 * w_y - halfSEq_3 * w_x;
 /*推定された四元数を計算*/
 SEq_1 += (SEqDot_omega_1 - (beta * SEqHatDot_1)) * deltat;
 SEq_2 += (SEqDot_omega_2 - (beta * SEqHatDot_2)) * deltat;
 SEq_3 += (SEqDot_omega_3 - (beta * SEqHatDot_3)) * deltat;
 SEq_4 += (SEqDot_omega_4 - (beta * SEqHatDot_4)) * deltat;
 /*四元数を正規化する*/
 norm = sqrt(SEq_1 * SEq_1 + SEq_2 * SEq_2 + SEq_3 * SEq_3 + SEq_4 * SEq_4);
 SEq_1 /= norm;
 SEq_2 /= norm;
 SEq_3 /= norm;
 SEq_4 /= norm;
 /*地球フレームでフラックスを計算する*/
 SEq_1SEq_2 = SEq_1 * SEq_2;  //axulirary変数を再計算する
 SEq_1SEq_3 = SEq_1 * SEq_3;
 SEq_1SEq_4 = SEq_1 * SEq_4;
 SEq_3SEq_4 = SEq_3 * SEq_4;
 SEq_2SEq_3 = SEq_2 * SEq_3;
 SEq_2SEq_4 = SEq_2 * SEq_4;
 h_x = twom_x * (0.5f - SEq_3 * SEq_3 - SEq_4 * SEq_4) + twom_y * (SEq_2SEq_3 - SEq_1SEq_4) + twom_z * (SEq_2SEq_4 + SEq_1SEq_3);
 h_y = twom_x * (SEq_2SEq_3 + SEq_1SEq_4) + twom_y * (0.5f - SEq_2 * SEq_2 - SEq_4 * SEq_4) + twom_z * (SEq_3SEq_4 - SEq_1SEq_2);
 h_z = twom_x * (SEq_2SEq_4 - SEq_1SEq_3) + twom_y * (SEq_3SEq_4 + SEq_1SEq_2) + twom_z * (0.5f - SEq_2 * SEq_2 - SEq_3 * SEq_3);
 /*磁束ベクトルを正規化してxとzの成分のみを持つようにする*/
 b_x = sqrt*1;
 b_z = h_z;}

void setup() {}

void loop () {}
イメージ 1
図2：C言語で最適化されたMARG用Madgwickフィルタ

2.2 調整可能なパラメータ
 調整可能なフィルタのパラメータ「β」の効果を図3に示します。
 静的および動的性能は、対応するRMS値の平均として定量化しており、「β」には明確な最適値があります。
 積分ドリフトによる誤差を最小限に抑えるのに十分高いが、勾配降下反復の大きなステップによって不要なノイズが導入されない程度に十分に低い。
イメージ 2
図3：MadgwickフィルタIMU（左）およびMARG（右）の性能に対する調整可能なパラメータβの効果

2.3 低いサンプリングレートで有効
 実験データを間引き1Hzと512Hzとの間のサンプリングレートをシミュレートした結果を図4に示す。
 Madgwickフィルタは、512Hzと同様に50Hzで同等の性能レベルを示す。
※10 Hzでサンプリングしている間において静的誤差<2◦ 動的誤差<7◦
イメージ 1
図4：MadgwickフィルタIMU（左）およびMARG（右）実装の性能に対するサンプリングレートの影響

2.4 従来のKalmanベースのアルゴリズムの精度を超える性能
 図5の黒実線は「光学的に測定された正確な実測値」、赤点線は「Kalmanフィルタによる推定方向」、青点線は「Madgwickフィルターによる推定方向」を示す。
 上グラフは実測及び推定された角度θ、下グラフは実測値に対する推定された角度の誤差を表す。
 下グラフより、「Madgwickフィルター」は「Kalmanフィルタ」より実測値により近い値を示している。
イメージ 3
図5：測定角度と推定角度θ（上）と誤差（下）の典型的な結果

表1：Kalmanベースのアルゴリズムと提案されたフィルタIMUおよびMARG実装の静的および動的RMS誤差
イメージ 4
※MARGセンサーに関する記事一覧はコチラ

3. まとめ

  Madgwickフィルターは「早い・簡単・高精度」！と三拍子揃った素晴らしい三次元姿勢推定フィルターですね
 このフィルターでドローンの姿勢がリアルタイムに分かれば、それを元に変則的な風が吹いたとしても、プロペラの浮力が変化したとしても姿勢を一定に保つ事が出来そうです！

イメージ 1イメージ 3
励みになりますのでよければクリック下さい(^o^)/

*1:h_x * h_x) + (h_y * h_y