■tan関数
tan関数は角度(ラジアン※1)から正接(tangent)※2を計算する三角関数※3です。
■使用例
Arduino IDEで使用するtan関数の使い方は以下の通りです。試しにこのプログラムをArduino UNOで実行すると、図1の様にシリアルモニタ上にtan(-135)の値が「Y/X = 1 : tan(Rad) = 1 : tan(Rad) = 1」と出力されます。

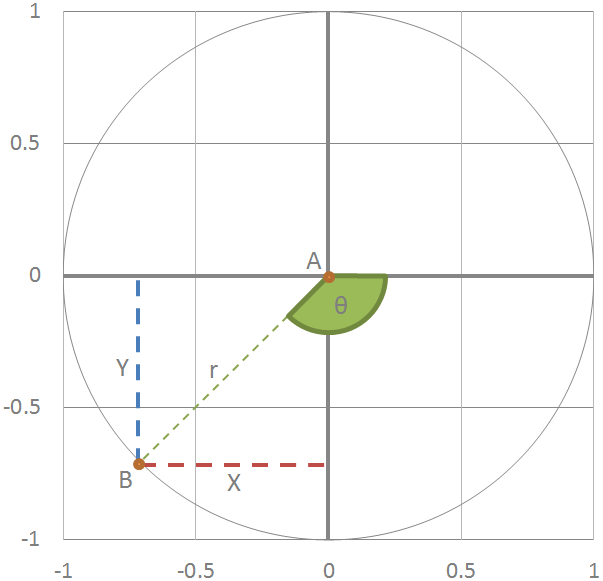
#define PI 3.141592653589793 //もしくは float PI=atan(1)*4; void setup() { Serial.begin(9600); //9600bpsでシリアルポートを開く } void loop() { //{}内を無限ループで実行する /*二点の座標から正接を計算*/ float XA = 0, //点ABのXY座標と半径rを宣言 YA = 0, XB = -0.707107, YB = -0.707107, X, Y, r; X = XB - XA; //点A→BのベクトルX成分を計算 Y = YB - YA; //点A→BのベクトルY成分を計算 r = sqrt(pow(X, 2) + pow(Y, 2));//ベクトル(XY)から半径rを計算 Serial.print("Y/X = "); //"Y/X = "をシリアル出力 Serial.print(Y / X); //Y/Xをシリアル出力 float deg = -135, Rad; //点ABの角度θの度とラジアンを宣言 /*PIを使って角度(度)から正接を計算(先頭の「#define PI」 が必要)*/ Rad = deg / (180 / PI); //度をラジアンに変換 Serial.print(" : tan(Rad) = "); //" : cos(Rad) = "をシリアル出力 Serial.print(tan(Rad)); //tan(Rad)をシリアル出力 /*atanを使って角度(度)から正接を計算(先頭の「#define PI」 は不要)*/ Rad = deg / (45 / atan(1)); //1rad=180/PI=45/atan(1)=57.296…° Serial.print(" : tan(Rad) = "); //" : tan(Rad) = "をシリアル出力 Serial.println(tan(Rad)); //tan(Rad)をシリアル出力 delay(1000); //1000ms(1秒)待ちます }

図1:プログラム例

図2:プログラム実行結果
■構文
tan(rad)
■パラメータ
rad :角度の単位はラジアンで変数の型はfloatです。
■戻り値
正接を表す数値 (double)、ラジアン・度・tanθの関係は表1の通りです。
※π=3.14159…
■補足
「円の半径に等しい長さの弧の中心に対する角度」と定義されています。
ラジアンと度の関係を表したものを表2に示します。
図2:ラジアンによる円周上の角度(単位:rad)
| 項目 | 内容 |
| 0 | 0 |
| 1 | 57.296… |
| n | 180 |
| 2n | 360 |
※π=3.14159…
直角三角形で一つの鋭角について、斜辺に対する底辺の比を示したもので余弦定理と言い、cos(コサイン)がつかわれます。
※3:三角関数とは?
三角関数(さんかくかんすう、英: trigonometric function)とは、平面三角法における、角の大きさと線分の長さの関係を記述する関数です。
励みになりますのでよければクリック下さい(^o^)/